¿QUE ES EL ÁLGEBRA LINEAL?
El álgebra lineal es la rama de las matemáticas que estudia conceptos tales como:Vectores,matrices,espacios vectoriales,y sus transformaciones lineales.Es un-área activa que contiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.
 |
 |
CAMPOS DE APLICACIÓN DEL ÁLGEBRA LINEAL
Es una herramienta de uso ineludible para el estudio de muchas otras materias que conforman el diseño curricular de un estudiante de ingeniería. Tiene una gran cantidad de aplicaciones en otras áreas, entre las cuales podemos mencionar la:
- Industria espacial
- Los circuitos electrónicos
 |
- Las redes de comunicación
 |
- La arqueología
 |
- La predicción del tiempo
 |
- Los movimientos de población
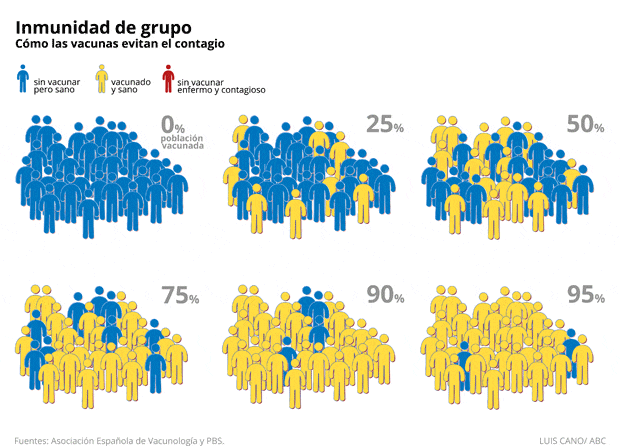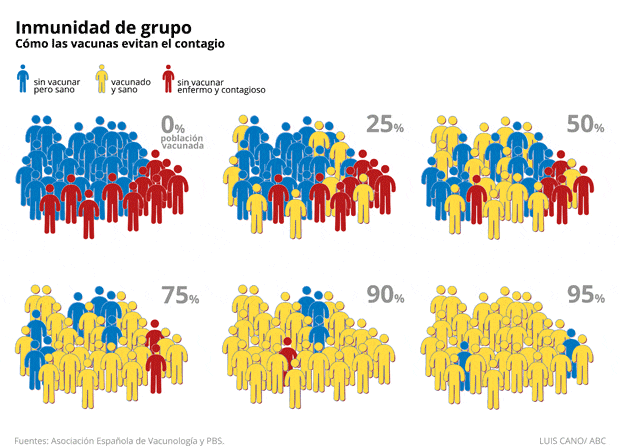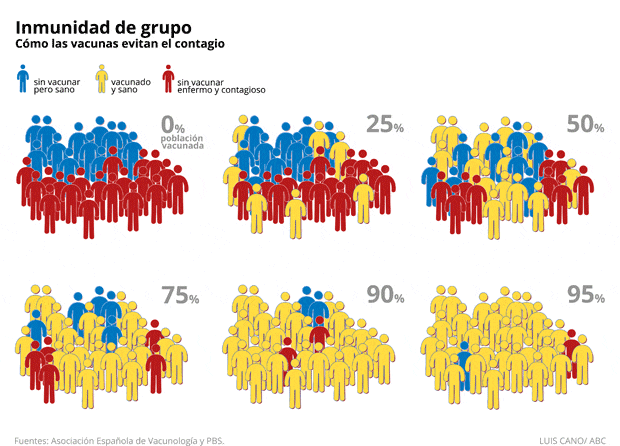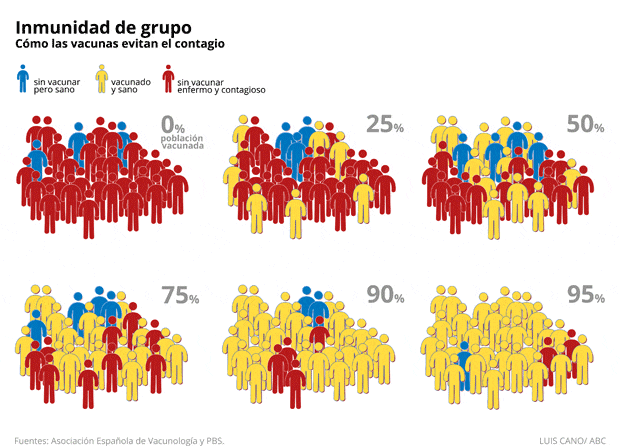 |
- La relatividad
 |
¿QUE SON LOS VECTORES?
- EN MEDICINA, vector es todo ser vivo y orgánico capaz de transmitir enfermedades de un ser enfermo a otro no para infectarlo, por ejemplo: el vector del dengue y de la fiebre amarilla es el mosquito aedes aegypti.
 |
- EN FÍSICA, vector es un segmento de recta orientado que permite representar las magnitudes vectoriales. También, es toda grandeza que puede ser medida, tomando en cuenta dirección, sentido y módulo. Por ejemplo: la velocidad o la fuerza.
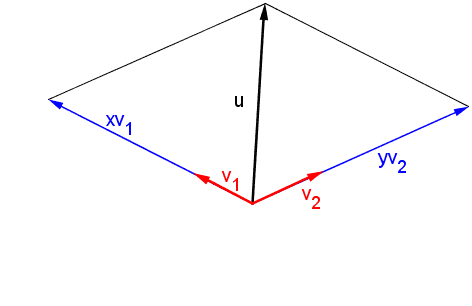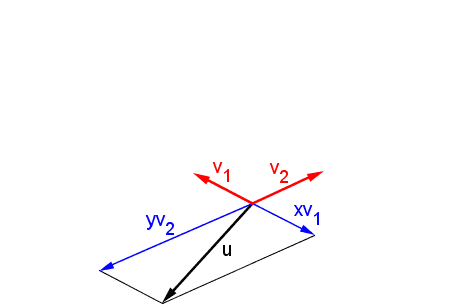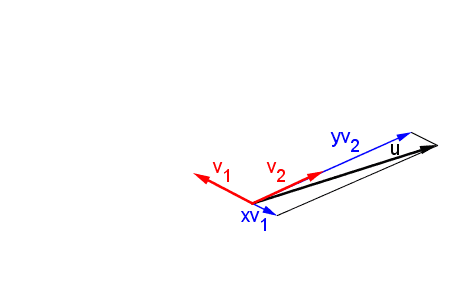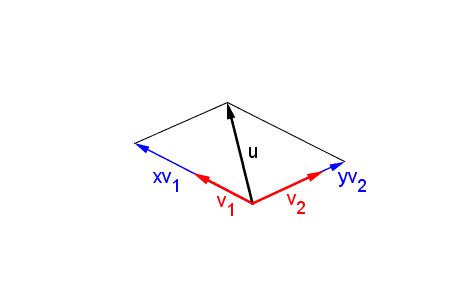 |
- EN MATEMATICA, en el área de cálculo vectorial, vector es un segmento de recta orientado, que depende de un sistema de coordenadas, en el cual se puede llevar un importante número de operaciones matemáticas, como suma, resta, descomposición, ángulo entre dos vectores, etc.
 |
- EN INFORMÁTICA, se define como vector a una zona de almacenamiento contiguo, ordenados en filas y/o columnas del mismo tipo y se hace referencia a cada uno de ellos por medio de un índice, también son llamados estructuras homogénea de datos. En referencia a este punto, existe vectores dinámicos (contiene una gran cantidad variable de datos) y vectores estáticos (contiene una cantidad fija de memoria).
 |
OPERACIONES EN LOS VECTORES
Supongamos que tenemos dos vectores u y v expresados a partir de sus vectores constituyentes en dos dimensiones para simplificar:
Suma de vectores
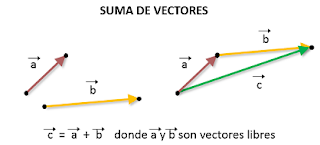 |
Se define el vector suma de ambos (w) a otro vector cuyas componentes se calculan sumando las componentes de cada uno de ellos.
Se puede apreciar según el dibujo que gráficamente esto equivale a colocar un vector a continuación del otro y dibujar el vector desde el origen del primero al final del segundo.
Producto escalar (·)
El producto escalar de dos vectores u y v que forman un ángulo φ se define como:
De la expresión anterior se observa que el producto escalar de dos vectores no es un vector, es un número (un escalar). Además el producto escalar de dos vectores perpendiculares es nulo. Se deducen entonces los siguientes resultados:
Si los vectores están expresados en componentes, en tres dimensiones y aplicando los resultados anteriores se obtiene que:
El producto escalar de dos vectores posee la propiedad conmutativa.
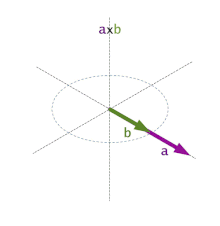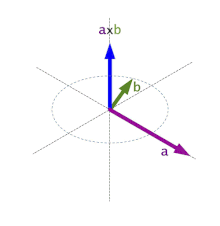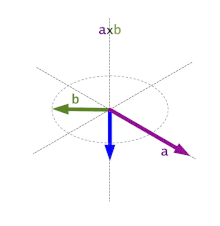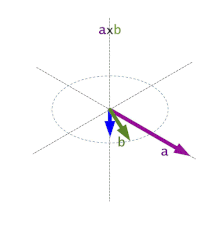
Producto vectorial (x)
El producto vectorial de dos vectores que forman un ángulo φ es otro vector, de dirección perpendicular al plano formado por los dos vectores, sentido el que da la regla de la mano derecha y módulo el que se especifica a continuación:
El producto vectorial no posee la propiedad conmutativa, ya que se cumple que:
Además, se cumple que el producto vectorial de dos vectores paralelos es nulo. Se obtienen entonces las siguientes relaciones:
Si los vectores vienen expresados en componentes el producto vectorial se calcula desarrollando el determinante:
VÍDEO SOBRE LAS OPERACIONES EN LOS VECTORES
¿QUE SON LAS MATRICES?
Una matriz es un conjunto de números reales, que están dispuestos en «m» filas y en «n» columnas: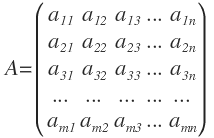 A los números que forman la matriz se les llama elementos.
A los números que forman la matriz se les llama elementos.
El número de filas por el número de columnas se denomina dimensión de la matriz y se designa como m x n, siendo m el número de filas y n el número de columnas.
Por ejemplo, estas son matrices de diferentes dimensiones:
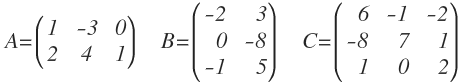
Donde la matriz A es una matriz de 2×3 (2 filas y 3 columnas), la matriz B es una matriz de 3×2 (3 filas y 2 columnas) y la matriz C es una matriz de 3×3 (3 filas y 3 columnas).
Las matrices son utilizadas en el álgebra lineal, una de las ramas del álgebra
TIPOS DE MATRICES
Matriz fila: matriz que solo tiene una fila


Matriz columna: matriz que solo tiene una columna


Matriz nula: todos sus elementos valen cero


Matriz cuadrada: igual número de filas que de columnas
Los siguientes tipos de matrices sólo son aplicables para matrices cuadradas:

Matriz simétrica: una matriz cuadrada es simétrica cuando los elementos a ambos lados de la diagonal principal son iguales.


Matriz antisimétrica (o hemisimétrica): matriz cuadrada en la que los elementos a ambos lados de la diagonal principal son opuestos (iguales pero con distinto signo).

Matriz diagonal: matriz cuadrada donde los elementos que no están en la diagonal principal son cero.


Matriz escalar: matriz cuadrada donde los elementos que no están en la diagonal principal son cero y los elementos de la diagonal principal son iguales


Matriz identidad o unidad: matriz cuadrada donde los elementos de la diagonal principal son unos y el resto ceros. Se representa por 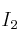 la matriz identidad de orden 2,
la matriz identidad de orden 2, 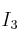 la identidad de orden 3,
la identidad de orden 3, 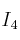 la de orden 4, etc.
la de orden 4, etc.





Matriz triangular superior: todos los elementos por debajo de la diagonal principal son cero.


Matriz triangular inferior: todos los elementos por encima de la diagonal principal son cero.


OPERACIONES ENTRE MATRICES
Suma de matrices
Dadas dos o más matrices del mismo orden, el resultado de la suma es otra matriz del mismo orden cuyos elementos se obtienen como suma de los elementos colocados en el mismo lugar de las matrices sumandos.
Ejemplo:
 |
Resta de matrices
Dadas dos o más matrices del mismo orden, el resultado de la resta es otra matriz del mismo orden cuyos elementos se obtienen como la resta de los elementos colocados en el mismo lugar de las matrices sumandos.
Ejemplo:
Multiplicación por un número
Para multiplicar una matriz cualquiera por un número real, se multiplican todos los elementos de la matriz por dicho número.
Ejemplo:
 |
Producto de matrices
El resultado de multiplicar dos matrices es otra matriz en la que el elemento que ocupa el lugar cij se obtiene sumando los productos parciales que se obtienen al multiplicar todos los elementos de la fila “i” de la primera matriz por los elementos de la columna “j” de la segunda matriz. Es decir, multiplicamos la primera fila por los elementos de la primera columna y el resultado será nuestro nuevo elemento. Para ello, el número de columnas de la primera matriz debe coincidir con el de filas de la segunda. Si no fuese así no podríamos realizar la operación.
Ejemplo:
 Observamos como la matriz resultante tiene el número de filas de la primera y el de columnas de la segunda.
Debemos recordar, que las matrices no tienen la propiedad conmutativa. En el caso de que se pudiera operar A.B y B.A el resultado por lo general puede ser diferente.
Observamos como la matriz resultante tiene el número de filas de la primera y el de columnas de la segunda.
Debemos recordar, que las matrices no tienen la propiedad conmutativa. En el caso de que se pudiera operar A.B y B.A el resultado por lo general puede ser diferente.
EJERCICIOS 

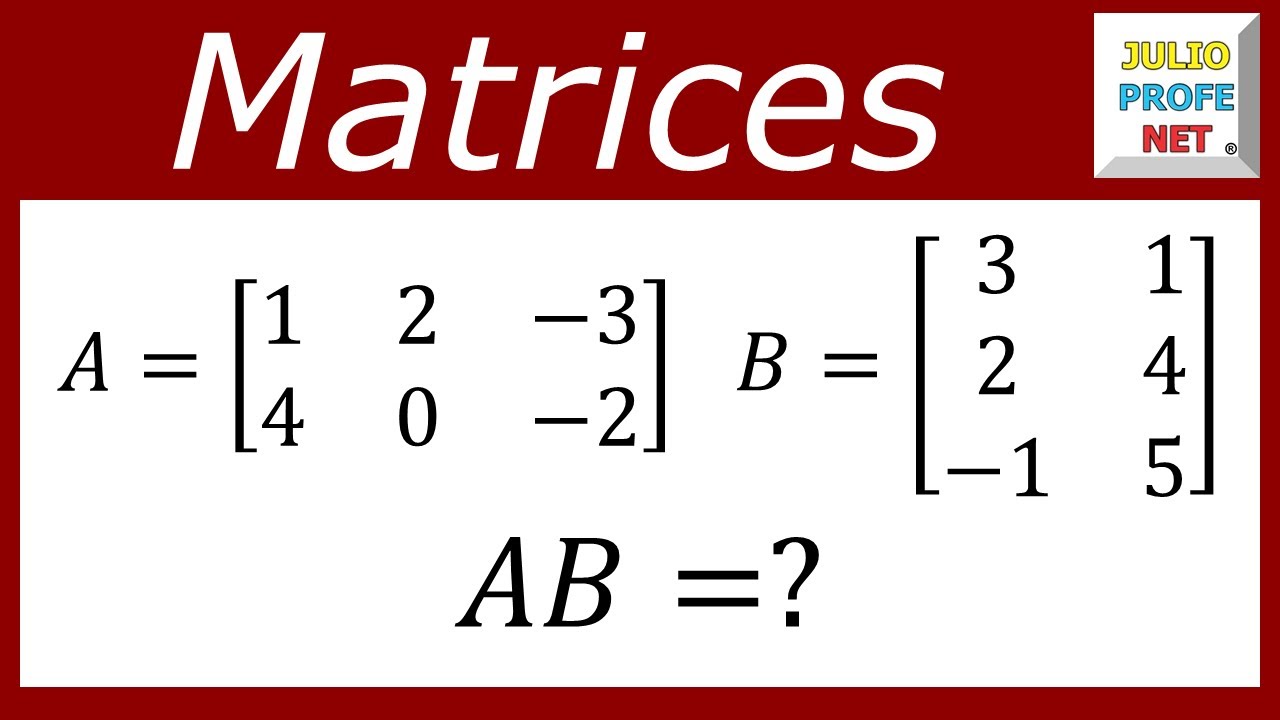
REDUCCIÓN DE MATRICES
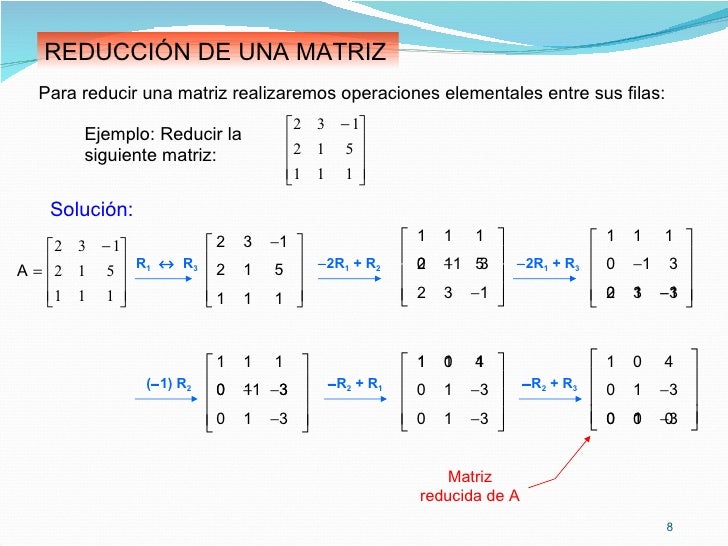
Se dice que es una matriz reducida si satisface las siguientes condiciones: 1) El primer elemento no nulo de cualquier fila no nula debe debe ser 1, mientras todos los demas elementos en la columna en que aparece este 1, deben ser ceros.
2) En cada fila, el primer elemento diferente de cero debe estar a la derecha del primer elemento no nulo de cada fila superior
3) TODAS LAS FILAS CUYOS ELEMENTOS: Todas las filas cuyos elementos son unicamente ceros deben estar en la parte inferior de la matriz
 |
METODO DE GAUUS- JORDAN O ELIMINACION DEL GAUSS-JORDAN
El método consiste en aplicar operaciones elementales fila, es decir, cualquier fila se puede multiplicar por cualquier número (distinto de cero) o se le puede sumar o restar cualquier otra fila multiplicada o no por cualquier número. No se puede restar una fila a ella misma. También puede intercambiarse el orden de las filas (por ejemplo, intercambiar las dos primera filas).
El proceso debe aplicarse hasta que se obtenga la matriz en forma escalonada (método de Gauss) o en forma escalonada reducida (método Gauss-Jordan) de la matriz ampliada.
Recordamos que una matriz en su forma escalonada reducida cumple:

Multiplicamos la primera fila por 1/5 y la segunda por 1/3
Multiplicamos la primera fila por 1/5 y la segunda por 1/3
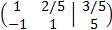
Sumamos a la segunda fila la primera
Sumamos a la segunda fila la primera
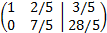
Multiplicamos la segunda fila por 5/7
Multiplicamos la segunda fila por 5/7
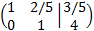
Sumamos a la primera fila la segunda fila multiplicada por -2/5
Sumamos a la primera fila la segunda fila multiplicada por -2/5
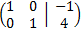
Ahora escribimos el sistema que representa esta última matriz:
Ahora escribimos el sistema que representa esta última matriz:
- En cada fila, el primer elemento distinto de cero (de izquierda a derecha) es un 1 (uno principal). A la izquierda de este 1, sólo hay ceros. A su derecha puede haber cualquier número. En la columna del 1 principal de las filas de arriba y las de abajo sólo puede haber ceros (a no ser que sea la primera fila y por encima del 1 no hay ningún elemento).
- El uno principal de cualquier fila se sitúa más a la izquierda de los unos principales de las filas inferiores a ésta.
- Si existen filas formadas únicamente por ceros, éstas son las inferiores.

Multiplicamos la primera fila por 1/5 y la segunda por 1/3
Multiplicamos la primera fila por 1/5 y la segunda por 1/3
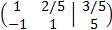
Sumamos a la segunda fila la primera
Sumamos a la segunda fila la primera
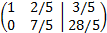
Multiplicamos la segunda fila por 5/7
Multiplicamos la segunda fila por 5/7
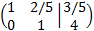
Sumamos a la primera fila la segunda fila multiplicada por -2/5
Sumamos a la primera fila la segunda fila multiplicada por -2/5
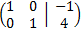
Ahora escribimos el sistema que representa esta última matriz:
Ahora escribimos el sistema que representa esta última matriz:
Es decir, hemos obtenido la solución del sistema.
No hay comentarios:
Publicar un comentario